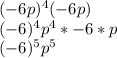Question

Simplify the expression.​ (Do not evaluate the exponents on coefficients in the​ answer.)


`(-6p)^(4) (-6p)`

(Type your answer using exponential​ notation.)

Answer 1

`(-6)^5p^5`

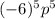
Explanation:

To evaluate or simplify expressions with exponents, we use exponent rules.

1. An exponent is only a short cut for multiplication. It simplifies how we write the expression.

2. When we multiply terms with the same bases, we add exponents.

3. When we divide terms with the same bases, we subtract exponents.

4. When we have a base to the exponent of 0, it is 1.

5. A negative exponent creates a fraction.

6. When we raise an exponent to an exponent, we multiply exponents.

7. When we have exponents with parenthesis, we apply it to everything in the parenthesis.

We will use these rules 2 and 7 to simplify. First apply the 4 exponent to both -6 and p. Then add the exponent of the base -6 and p on the outside of the parenthesis.

`(-6p)^4(-6p)\\(-6)^4p^4*-6*p\\(-6)^5p^5`