If
 and
and
 are continuous everywhere, that means that for any
are continuous everywhere, that means that for any
 , the limit as
, the limit as
 for either function is the value of that function at
for either function is the value of that function at
 :
:
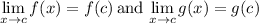
Applying some properties of limits, we can rewrite the original limit as

Given the continuity of
 and
and
 , we have
, we have
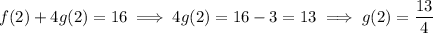
So for both parts, the answer is 13/4.