Question

An engineer is designing a storage compartment in a spacecraft .The compartment must be 2 meters longer than it is wide, and its depth must be 1 meter less than its width. The volume of the compartment must be 8 cubic meters.Write an equation to model the volume of the compartment. Determine the dimensions where it produces the maximum volume. Sketch the graph

Answer 1

Let x be the width of the compartment,

⇒ The length of the compartment = x + 2

⇒ the depth of the compartment = x -1

Thus, the volume of the compartment,
`V(x) = (x+2)x(x-1) = x^3 + x^2 - 2x`

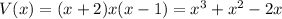
The volume of the compartment must be 8 cubic meters.

⇒
`x^3 + x^2 - 2x = 8`

⇒
`x^3 + x^2 - 2x - 8=0`

⇒
`(x-2)(x^2+3x+4)=0`

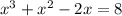
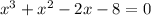
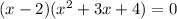
If
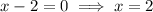`x-2=0\implies x = 2` and if
`x^2+3x+4=0\implies x = \text{a complex number}`

But, we can not take width as a complex number.

⇒ Width of the compartment = 2 meter.

Length of the compartment = 2 + 2 = 4 meter.

Depth of the compartment = 2 - 1 = 1 meter.

Here, the function that shows the volume of the compartment is,

`V(x) = x^3 + x^2 - 2x`

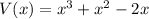
When we lot the graph of that function we found,

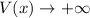`V(x)\rightarrow + \infty` as
`x\rightarrow + \infty`

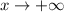
But we can not take width as infinite.

Therefore, the maximum value of V(x) will be 8 at x = 2.