Question

Which statement could be used to explain why f(x) = 2x – 3 has an inverse relation that is a function? The graph of f(x) passes the vertical line test. f(x) is a one-to-one function. The graph of the inverse of f(x) passes the horizontal line test. f(x) is not a function.

Answer 1

f(x) is a one to one function.That maps out one function to another ,and it therefore passes both the vertical and horizontal I ine test

Answer 2

Answer with explanation:

The given linear function is

f(x)= 2 x -3

y=2 x -3

`y+3=2x\\\\x=(y+3)/(2)`

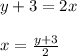
Replacing , x by y, and y by x, we will get the Inverse of the given function

`y=(x+3)/(2)`

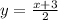
Since ,for every x, there is a unique y, or for every, y there is unique x, therefore it is a function.

We can check this also by using the concept of function, that is the function must be one one and Onto.

To check whether, the linear function is one- one,

If ,f(a)=f(b), then , a=b.

f(a)= 2 a -3

f(b)=2 b -3

2 a -3 = 2 b -3

2 a= 2 b

a=b

So, f(x)=2 x -3, is one -one.

To Check whether it is onto

for, f(x)=y

there must be unique x, for unique y

`y=(x+3)/(2)`

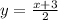
So , f(x) is one one and onto.Which shows that f(x) has an Inverse.

Otherwise , we will use Horizontal line test.

Draw the graph of , f(x)=2 x -3

Horizontal lines does not cut the function, more than once.

or, you can find the inverse of f(x),then check whether it passes Horizontal line test.That is, function , 2 y = x +3, the inverse function Passes Horizontal Line test.

Option C: The graph of the inverse of f(x) passes the horizontal line test.