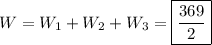Parameterize each line segment from
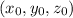 to
to
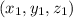 by
by
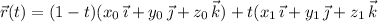
with
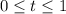 . The work done by
. The work done by
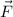 on the particle along each segment is given the line integral of
on the particle along each segment is given the line integral of
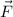 with respect to that segment,
with respect to that segment,
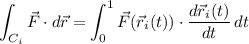
• (3, 0, 0) to (3, 5, 1)
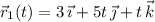
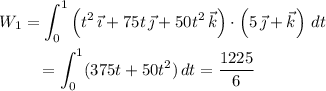
• (3, 5, 1) to (0, 5, 1)
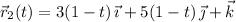
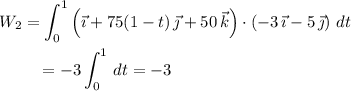
• (0, 5, 1) to (0, 0, 0)
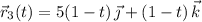
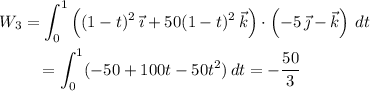
Then the total work done by
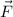 on the particle is
on the particle is