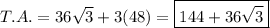Look at the picture.
We have in a base an equilateral triangle.
The formula of the area of an equilateral triangle:
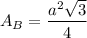
We have a = 12. Substitute:
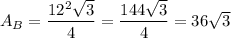
The lateral side is a isosceles triangle. The formula of the area of a triangle is:

We must calculate the length of h using the Pythagorean theorem:
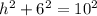
 subtract 36 from both sides
subtract 36 from both sides
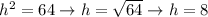
We have b = 13 and h = 8. Substitute:

The Total Area:
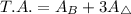
Substitute: