Answer:
As per the given statement:
The distance from jack eyes to the top of the tower = 50.64 m
Also, jack and john eyes are 1.5 m from the ground.
Labelled diagram as shown in the attachment
Let BC = x m be the distance of the jack from the base of the tower and
AG = y m be the distance above 1.5 m from the the ground.
Using tangent ratio:
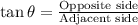
In triangle AGE;
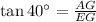
Here, AG = y m and EG = 20+x m
then;

or we can write this as;
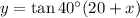 ........[1]
........[1]
Similarly, in AGF;

then;
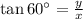

or
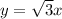 ......[2]
......[2]
Substitute equation [2] into the equation [1], to solve for x;
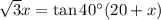
or
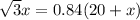
Using distributive property:
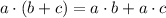
we have;
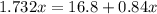
Subtract 0.84 x from both sides we get;

Divide both sides by 0.892 we get;
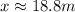
Therefore, 18.8 meter johns from the base of the tower.