Question

Determine if segments AB and CD are parallel, perpendicular, or neither

1. Line AB formed by A(-1,3) and B(1,5); Line CD formed by C(2,3) and D(-2,7)

2. Line AB formed by A(3,8) and B(-6,5); Line CD formed by C(-6,7) and D(-3,8)

3. Line AB formed by A(2,-7) and B(2,3); Line CD formed by C(-4,0) and D(-4,-5)

Answer 1

1 is perpendicular

2 is parallel

3 is parallel

Explanation:

yeah

Answer 2

1: perpendicular.

2 and 3: parallel.

Explanation:

Given line segment AB and CD, in each part we have to find the slope in order to find the nature i.e these are parallel, perpendicular, or neither

we know Two lines are parallel if they have same slope, perpendicular if their slopes are negative reciprocals.

1. Line AB formed by A(-1,3) and B(1,5); Line CD formed by C(2,3) and D(-2,7)

Slope of AB is
`(y_(2)-y_(1))/(x_(2)-x_(1))=(5-3)/(1-(-1))=1`

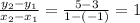
Slope of CD is
`(y_(2)-y_(1))/(x_(2)-x_(1))=(7-3)/(-2-(2))=-1`

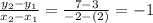
The slopes of above two are negative reciprocals. Hence, the lines are perpendicular.

2. Line AB formed by A(3,8) and B(-6,5); Line CD formed by C(-6,7) and D(-3,8)

Slope of AB is
`(y_(2)-y_(1))/(x_(2)-x_(1))=(5-8)/(-6-(3))=(1)/(3)`

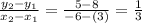
Slope of CD is
`(y_(2)-y_(1))/(x_(2)-x_(1))=(8-7)/(-3-(-6))=(1)/(3)`

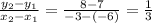
The slopes of above two are equal. Hence, the lines are parallel.

3. Line AB formed by A(2,-7) and B(2,3); Line CD formed by C(-4,0) and D(-4,-5)

Slope of AB is
`(y_(2)-y_(1))/(x_(2)-x_(1))=(3+7)/(2-2)=\infty`

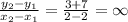
Slope of CD is
`(y_(2)-y_(1))/(x_(2)-x_(1))=(-5-0)/(-4+4)=\infty`

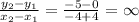
The slopes of above two lines are undefined. Hence, these are vertical lines therefore parallel.