Answer: 13.5 inches.
Explanation:
Given : The volume of a right circular cone varies jointly as the altitude and the square of the radius of the base.
V α r² h , where r= radius and h = height.
i.e. V = k r² h (1), where c is the constant of proportionality.
When the volume of the cone is 154 cu. in. when its altitude is 12 in. and the radius of the base is
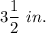 .
.
Put
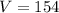 ,
,
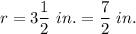 and h = 12
and h = 12
in (1) , we get
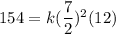
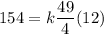
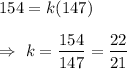
When the volume of the cone is 77 cu. in. and the radius of the base is
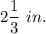
Put V = 77 ,
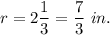 and
and
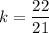 in (1) , we get
in (1) , we get


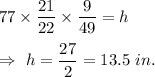
Hence, the altitude = 13.5 inches.