Question

What conclusions can you draw about the relationship between arithmetic or geometric sequences and linear or exponential functions?

Practice
Answer in complete sentences.

Answer 1

Relationship between:

Arithmetic or geometric sequences and Linear or exponential function

• Arithmetic sequence is same as linear function with the common difference as a slope.

• Geometric sequence is obtained from exponential function by replacing the variable x by n integer.

• Linear function take the form:
  `y =mx+b`.

• Linear function changes at a constant rate per unit interval.

• Exponential function take the form:
  `y = ab^x`.

• Exponential function changes by a common ratio over an interval.

If you look the graph of the arithmetic sequence, they are always linear

and the graph of the geometric sequence are always exponential.

Answer 2

→→Arithmetic sequence: When we talk about arithmetic sequence . there is a thing called Common Difference , which can be calculated by finding the difference between two consecutive terms, that is the beginning term and it's Succeeding term.

→n th term of Arithmetic sequence= A + (n-1) d, Here A= First term, d=Common Difference

If value of n changes ,that is for different positive integral values of n, we get different terms in a sequence.

→→→If we compare it with , linear function, which is represented as

→y= m x + c, here m= Slope of line, C= Y intercept

So, if slope of line changes , we get different equation of line.

→→When we talk about geometric sequence, the word comes into notion is Common ratio, which can be calculated by dividing the succeeding term by preceding term.

→→General formula for Geometric Sequence =
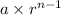`a * r^(n-1)`, where a = First term , r= Common ratio

For, r> 1, each succeeding term increases by a fixed value called common ratio, and when r<1, each succeeding term is less than by it previous term by a fixed quantity, called common ratio.

→→Similarly, exponential function behaves in same way.

General formula for exponential functions =
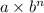`a * b^(n)`, or
`a * b^(-n)` where a = Starting term

Keeping the value of b and ,a fixed, if n is positive , graph of the function is Strictly increasing,and if n is negative graph of function is strictly decreasing.