Question

((Picture) CONVERGENT AND DIVERGENT SERIES PLEASE HELP!!

Answer 1

This series is divergent

B.

Explanation:

We are given a series

Firstly, we will find nth term

Numerator:

2 , 4, 8 , 16 , .....

`a_n=2^n`

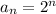
Denominator:

1^2 , 2^2 , 3^2 , ....

`b_n=n^2`

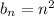
now, we can find nth term

`c_n=(2^n)/(n^2)`

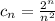
We can use ratio test

`L= \lim_(n \to \infty) c_n= \lim_(n \to \infty) ((2^(n+1))/((n+1)^2))/((2^n)/(n^2))`

`L=\lim _(n\to \infty \:)\left((2n^2)/(\left(n+1\right)^2)\right)`

`L=2\left(\lim _(n\to \infty \:)\left((1)/(1+(1)/(n))\right)\right)^2`

`L=2\left((1)/(1)\right)^2`

`L=2>1`

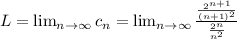
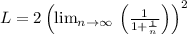
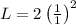
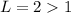
Since, it is greater than 1

so, this series is divergent