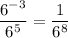Question

Simplify 6 to the negative 3rd power over 6 to the 5th. 68 6−2 1 over 6 to the 8th power 1 over 6 to the 2nd power

Answer 1

The simplified expression is given by:

1 over 6 to the 8th power.

`(1)/(6^8)`

Explanation:

We are asked to simplify the expression:

6 to the negative 3rd power over 6 to the 5th power.

which is mathematically written as:

`(6^(-3))/(6^5)`

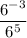
Now, we know that:

`(a^m)/(a^n)=(1)/(a^(n-m))`

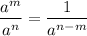
Here,

`m=-3\ and\ n=5`

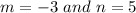
Hence, we get:

`(6^(-3))/(6^5)=(1)/(6^(5-(-3)))`

i.e.

`(6^(-3))/(6^5)=(1)/(6^(5+3))`

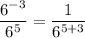
Hence, we get the simplified expression as follows:

`(6^(-3))/(6^5)=(1)/(6^8)`

Answer 2

`(1)/(6^8)`

Explanation:

`(6^(-3))/(6^5)=(1)/(6^(5+3))=(1)/(6^8)`

___

The applicable rules of exponents are ...

`a^(-b)=(1)/(a^b)\\\\a^b* a^c=a^(b+c)`