Answer:
Correct Answer is E(7.8\times10^{11} meters[/tex]
)
Step-by-step explanation:
In this question we have given,
Time period= 12 years (
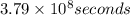 )
)
mass of the Sun, M =

Let m be the mass of jupiter
We know that,
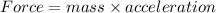
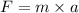 .............(1)
.............(1)
Also we know that,
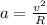
put values of m(mass of jupiter) and a in equation (1)
 ..............(2) (Direction of this force is toward sun)
..............(2) (Direction of this force is toward sun)
We know that Gravitational force between jupiter of mass m and sun of Mass M which are at distance R is given as
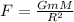 .............(3)(Direction of this force is toward sun)
.............(3)(Direction of this force is toward sun)
Here G is universal gravitational constants and its value is
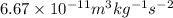
From equation (2) and equation (3)
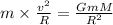
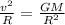
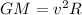 ...................(4)
...................(4)
We know that,
Time period
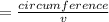

or
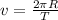
put value of v in equation (4)
we get,
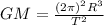
Therefore,
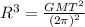 .............(5)
.............(5)
put values of G, M, T and
 in equation 5
in equation 5

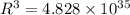
or,
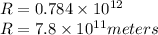
(in round figure 7.84 can be written as 7.8)