Question

The length of a rectangular flower garden is 5 feet more than its width. If the area of the garden is 104 square feet, what is the perimeter of the garden?

Answer 1

Explanation:

width= w

length = l=w+5

Area = l * w

104 =(w+5) * w

w2 +5w -104 =0

(w+13)(w-8)=0

w=13 and w=8

so width =8

length=13

Answer 2

42 feet.

Explanation:

Let w be width of rectangle.

We have been given that the length of a rectangular flower garden is 5 feet more than its width. So the length of garden would be
`w+5`.

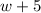We are also told that the area of the garden is 104 square feet.

We know that area of rectangle is length times width. We can represent our given information in an equation as:

`w(w+5)=104`

`w^2+5w=104`

`w^2+5w-104=0`

`w^2-8w+13w-104=0`

`w(w-8)+13(w-8)=0`

`(w-8)(w+13)=0`

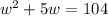
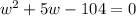
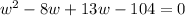
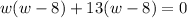
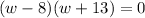
Zero product property:

`(w-8)=0\text{ or}(w+13)=0`

`w=8\text{ or}w=-13`

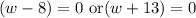
Length of rectangle
`w+5\Rightarrow 8+5=13`

Perimeter of rectangle
`2(\text{Length+Width})=2(21)=42`

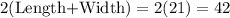
Therefore, the perimeter of rectangle is 42 feet.