Answer:
The correct option is C.
Explanation:
The given expression is
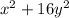
In option A,
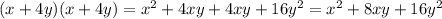
Therefore option A is incorrect.
In option B,
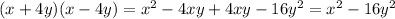
Therefore option B is incorrect.
In option D,
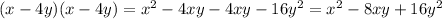
Therefore option D is incorrect.
Since the given expression can not be factored further, therefore it is a prime expression and option C is correct.