The formula for the circumference of a circle is c=rd, where d is the length of the diameter. If d is a rational number, what can you conclude about the circumference? It is a f…

Question

asked Jul 10, 2020 221k views

2 Answers

Vik Gamov · Answer 1 · 2020-07-12T20:12:30+0000

The statement that is true about the circumference of the circle is:

The formula for the circumference of a circle is :

c=πd where d is the length of the diameter.

and π is a irrational number.

If d is a rational number, then as we know that the multiplication of a rational and a irrational number is always irrational.

Hence, the value of circumference is an irrational number.

Hewo · Answer 2 · 2020-07-15T10:12:41+0000

Answer: The answer is (d) It is an irrational number.

Step-by-step explanation: Given formula for circumference of a circle is

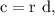
$\textup{c}=\textup{r d},$

where 'd' is the length of the diameter and a rational number.

We are to choose one of the given four options for the circumference 'c' of the circle.

We know that the circumference of a circle with diameter 'd' is given by

$\textup{c}=\pi \textup{d},$

Comparing this with the given equation, we get

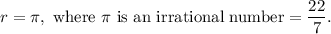
$r=\pi,~\textup{where}~\pi~\textup{is an irrational number}=(22)/(7).$

Now, the product of a rational and an irrational number is again irrational, so 'r × d' will be an irrational number.

Hence, the circumference, c = rd is irrational.

Thus, the correct option is (d) It is an irrational number.