Answer: The correct option is
(B)
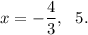
Step-by-step explanation: We are given to solve the following equation for x :
"2 over quantity x minus 2 plus 7 over quantity x squared minus 4 equals 5 over x."
The above equation can be written as :

We will be using the following formula to solve equation (i) :
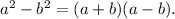
The solution of equation (i) is as follows :
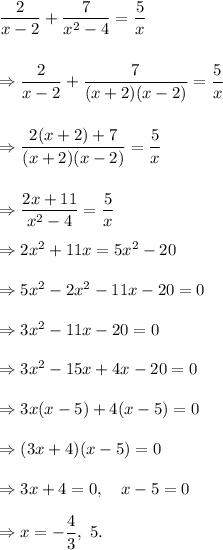
Thus, the required solution of the given equation is
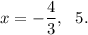
Option (B) is CORRECT.