Step by step solution :
standard deviation is given by :
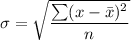
where,
 is standard deviation
is standard deviation
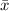 is mean of given data
is mean of given data
n is number of observations
From the above data,
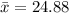
Now, if
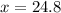 , then
, then
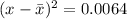
If
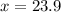 , then
, then
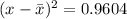
if
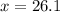 , then
, then
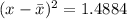
If
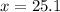 , then
, then
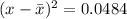
If
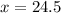 , then
, then
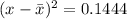
so,
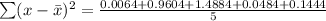
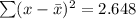
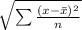
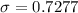
No, Joe's value does not agree with the accepted value of 25.9 seconds. This shows a lots of errors.