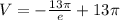Question

Use the method of cylindrical shells to find the volume V generated by rotating the region bounded by the given curves about the y-axis. y = 13 e**(-x**2) text(, ) y = 0 text(, ) x = 0 text(, ) x = 1 V = Sketch the region and a typical shell. (Do this on paper. Your instructor may ask you to turn in this sketch.)

Answer 1

To find the volume generated by rotating the region bounded by the curves y = 13 e^(-x^2), y = 0, x = 0, and x = 1 around the y-axis, we can use the method of cylindrical shells. By setting up the integral expression and evaluating the integral, we can find the volume.

Step-by-step explanation:

To find the volume generated by rotating the region bounded by the curves around the y-axis, we can use the method of cylindrical shells.

1. First, let's sketch the region and a typical shell. The region is bounded by the curves y = 13 e^(-x^2), y = 0, x = 0, and x = 1. The shell can be visualized as a thin cylindrical tube placed around the y-axis, perpendicular to the x-axis.
2. Next, we'll set up the integral expression for the volume of the region using cylindrical shells. The volume of a single shell is given by V = 2πrxh, where r is the distance from the y-axis to the shell, h is the height of the shell, and x is the coordinate along the x-axis. In this case, r = x, h = y, and we integrate with respect to x.
3. Now we can set up the integral: V = ∫[from 0 to 1] 2πxy dy. To evaluate this integral, we need to express y in terms of x using the given equation y = 13 e^(-x^2).
4. Finally, we evaluate the integral and find the volume V generated by rotating the region bounded by the given curves about the y-axis.

Answer 2

As per the given statement:

The region bounded by the given curves about the y-axis,
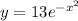`y = 13e^(-x^2)`, y=0, x = 0 and x = 1

Using cylindrical shell method:

The volume of solid(V) is obtained by rotating about y-axis and the region under the curve y = f(x) from a to b is;

`V = \int_(a)^(b) 2\pi x f(x) dx` where
`0\leq a<b`

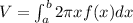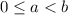
where x is the radius of the cylinder

f(x) is the height of the cylinder.

From the given figure:

radius = x

height(h) =f(x) =y=
`13e^(-x^2)`

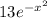
a = 0 and b = 1

So, the volume V generated by rotating the given region:

`V =2 \pi \int_(0)^(1) x ( 13e^(-x^2)) dx\\\\V=2\pi\left [ -(13)/(2)e^(-x^2) \right ]_(0)^(1)\\\\V=2\pi\left (-(13)/(2e)-\left(-(13)/(2)\right) \right )\\\\V=-(13\pi )/(e)+13\pi`

therefore, the volume of V generated by rotating the given region is
`V=-(13\pi )/(e)+13\pi`