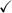Answer: (-1, -4) and (-2, -5)
Explanation:
Solve the second equation for y: y + 3 = x → y = x - 3
Use the substitution method. Replace "y" with "x - 3" in the first equation and solve for x.
y = x² + 4x - 1
x - 3 = x² + 4x - 1
0 = x² + 3x + 2
0 = (x + 1)(x + 2)
0 = x + 1 and 0 = x + 2
-1 = x and -2 = x
Next, plug the x-values (x = -1 and x = -2) into the first equation to solve for y.
y = x - 3 and y = x - 3
= (-1) - 3 and = (-2) - 3
= -4 and = -5
when x = -1, y = -4 and when x = -2, y = -5
Check:
Plug the x and y-values into the first equation to verify each solution makes a true statement.
y = x² + 4x - 1 y = x² + 4x - 1
-4 = (-1)² + 4(-1) - 1 -5 = (-2)² + 4(-2) - 1
-4 = 1 - 4 - 1 -5 = 4 - 8 - 1
-4 = -4
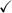-5 = -5