Question

Please. Physics is so difficult.

A pendulum on a grandfather clock is supposed to oscillate once every 2.00 s, but actually oscillates once every 1.99 s. How much must you increase its length to correct its period to 2.00 s?​

Answer 1

the answer should be 0.00988 m

Answer 2

0.010 m

Step-by-step explanation:

So the equation for a pendulum period is:
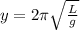`y=2\pi\sqrt{(L)/(g)}` where L is the length of the pendulum. In this case I'll use the approximation of pi as 3.14, and g=9.8 m\s. So given that it oscillates once every 1.99 seconds. you have the equation:

`1.99 s = 2(3.14)\sqrt{(L)/(9.8 m\backslash s^2)}\\`

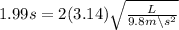
Evaluate the multiplication in front

`1.99 s = 6.28\sqrt{(L)/(9.8m\backslash s^2)`

Divide both sides by 6.28

`0.317 s= \sqrt{(L)/(9.8 m\backslash s^2)}`

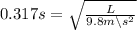
Square both sides

`0.100 s^2= (L)/(9.8 m\backslash s^2)`

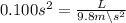
Multiply both sides by m/s^2 (the s^2 will cancel out)

`0.984 m = L`

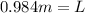
Now now let's find the length when it's two seconds

`2.00 s = 6.28\sqrt{(L)/(9.8m\backslash s^2)}`

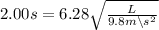
Divide both sides by 6.28

`0.318 s = \sqrt{(L)/(9.8 m\backslash s^2)`

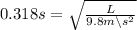
Square both sides

`0.101 s^2 = (L)/(9.8 m\backslash s^2)`

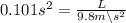
Multiply both sides by 9.8 m/s^2 (s^2 will cancel out)

`0.994 m = L`

So to find the difference you simply subtract

0.984 - 0.994 = 0.010 m