Question

Tickets at a particular movie theater have different rates for adults and children. On Friday, the theater sold 4 adult tickets and 7 child tickets for $83. The next day, the theater sold 5 adult tickets and 6 children tickets for $90. What is the price for the adult ticket and the price for the child ticket?

Answer 1

Answer: The price for the adult tickets is $12 and the price for the child ticket is $5.

Explanation:

Let the price for the adult ticket be x

Let the price for the child ticket be y

According to question, On Friday ,

`4x+7y=83`

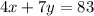
and on next day,

`5x+6y=90`

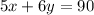
Now, we will use "Substitution Method" to solve the system of equations :

`5x+6y=90\\\\5x=90-6y\\\\x=(90-6y)/(5)`

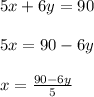
so, we will put the value of x in the first equation i.e.

`4x+7y=83\\\\4((90-6y)/(5))+7y=83\\\\360-24y+35y=83* 5\\\\35y-24y=415-360\\\\11y=55\\\\y=(55)/(11)\\\\y=5`

Now, put the value of y in the equation that is given by

`x=(90-6y)/(5)\\\\x=(90-6* 5)/(5)\\\\x=(90-30)/(5)\\\\x=(60)/(5)\\\\x=\$12`

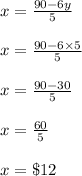
Hence, the price for the adult tickets is $12 and the price for the child ticket is $5.