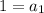Answer:
1
Explanation:
So the sum of a finite geometric series can be defined as:
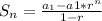 where r is the constant ratio or how much more greater the current term is, compared to the previous term (how much it's being multiplied by), and the n is the number of terms in the series. So with the given information you have the equation:
where r is the constant ratio or how much more greater the current term is, compared to the previous term (how much it's being multiplied by), and the n is the number of terms in the series. So with the given information you have the equation:
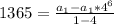
Simplify:
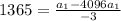
Multiply both sides by -3
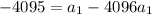
Subtract coefficients
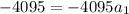
Divide both sides by -4095