Question

4 (Picture) CONVERGENT AND DIVERGENT SERIES PLEASE HELP!!

Answer 1

Option b is correct.

Divergent

Comparison Test:

Let
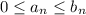`0\leq a_n\leq b_n` for all n.

If
`\sum_(n=1)^(\infty) b_n` converges, then
`\sum_(n=1)^(\infty) a_n` converges.

If
`\sum_(n=1)^(\infty) a_n` diverges, then
`\sum_(n=1)^(\infty) b_n` is also diverges.

Given the series
`(25)/(3) + (125)/(9) +(625)/(27)+....`

⇒
`a_n = (5^(n+1))/(3^n)` for all natural number n.

or

`a_n = 5((5^n)/(3^n))`

Note that:
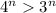`4^n > 3^n` for all natural number n.

then;

`(1)/(4^n)<(1)/(3^n)`

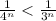
or

`(5^n)/(4^n)<(5^n)/(3^n)`

`5((5^n)/(4^n))<5((5^n)/(3^n))`

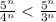
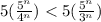
Geometric series:

`\sum_(n=1)^(\infty) ar^n`

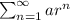
if
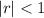`|r| < 1`, then the series is convergent.

if
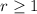`r\geq 1` then the series is divergent.

then;

by geometric series,
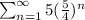`\sum_(n=1)^(\infty) 5((5)/(4))^n` it diverges as r > 1.

By comparison test:

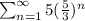`\sum_(n=1)^(\infty) 5((5)/(3))^n` diverges.

Therefore, the given series
`(25)/(3) + (125)/(9) +(625)/(27)+....` is divergent.