ANSWER
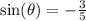
EXPLANATION
The cosine function is an even function.
It has the following property.
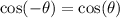
This implied that if

Then,
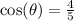
Using the Pythagorean identity,
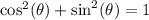
We substitute the value of
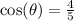
into the equation to get,
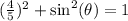
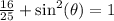

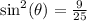
We take square root of both sides to get,
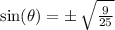
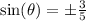
It was given that,
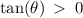
This implies that the angle is in the first quadrant. That is the only quadrant where both the cosine and the tangent ratios are positive.
Hence,
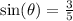
.
But the sine function is an odd function.
This means that,
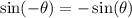
Therefore,
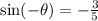
.