Question

5 (Picture) CONVERGENT AND DIVERGENT SERIES PLEASE HELP!!

Answer 1

Yes, this series converges. We can check using the integral test; we have

`\displaystyle\frac1{25}+\frac1{36}+\frac1{49}+\cdots=\sum_(n=5)^\infty\frac1{n^2}`

and

`\displaystyle\sum_(n=5)^\infty\frac1{n^2}\le\int_5^\infty(\mathrm dx)/(x^2)=\frac15`

Answer 2

Option A is correct.

True.

The series:
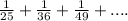`(1)/(25)+(1)/(36) +(1)/(49) +....` is convergent

Explanation:

Comparison Test:

Let
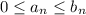`0\leq a_n\leq b_n` for all n.

If
`\sum_(n=1)^(\infty) b_n` converges, then
`\sum_(n=1)^(\infty) a_n` converges.

If
`\sum_(n=1)^(\infty) b_n` diverges, then
`\sum_(n=1)^(\infty) a_n` diverges.

Given the series:
`(1)/(25)+(1)/(36) +(1)/(49) +....`

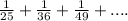
then;

`a_n = \sum_(n=1)^(\infty)(1)/((n+4)^2)`

`(1)/((n+4)^2) \leq (1)/(n^2)`

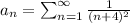
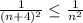
By comparison test:

`b_n = (1)/(n^2)`

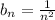
P-series test:

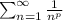`\sum_(n=1)^(\infty) (1)/(n^p)` where p> 0

If p>1 then the series converges and if 0<p< 1, then the series diverges.

By using p-test series in series
`b_n`

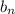
then;

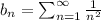`b_n = \sum_(n=1)^(\infty) (1)/(n^2)` is a p-series, with p> 1, it converges.

Comparing the above series with
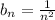`b_n = (1)/(n^2)`, we can conclude that
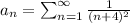`a_n = \sum_(n=1)^(\infty)(1)/((n+4)^2)` also converges and
`(1)/((n+4)^2) \leq (1)/(n^2)`

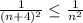
Therefore, the given series is convergent.