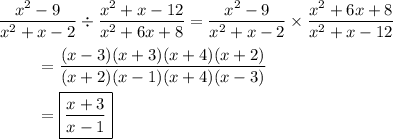Question

Please help me I am confused on how to do these.

Answer 1

1. There's so much wrong with the suggested solution that it's hard to pinpoint the exact error. The "logic" is inconsistent - why do the
`x` and constant term stay in the denominator but the
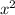`x^2` term does not?

What should be done is factorization in the numerator and denominator:

`x^2 + 2x - 8 = (x + 4) (x - 2)`

`x^2 + 6x - 16 = (x + 8) (x - 2)`

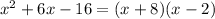
Then in the quotient, the factors of
`x-2` cancel so that

`(x^2+2x-8)/(x^2+6x-16) = ((x+4)(x-2))/((x+8)(x-2)) = \boxed{(x+4)/(x+8)}`

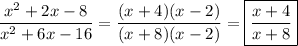
2. Use the same strategy: factorize everything everything you can, then cancel anything you can.

`x^2 - 9 = (x-3) (x+3)`

`x^2+x-2 = (x+2)(x-1)`

`x^2+x-12 = (x+4)(x-3)`

`x^2+6x+8 = (x+4)(x+2)`

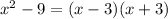
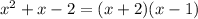
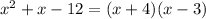
Then using the algebraic properties of multiplication/division, we have

`(x^2-9)/(x^2+x-2) / (x^2+x-12)/(x^2+6x+8) = (x^2-9)/(x^2+x-2) * (x^2+6x+8)/(x^2+x-12) \\\\ ~~~~~~~~= ((x-3)(x+3)(x+4)(x+2))/((x+2)(x-1)(x+4)(x-3)) \\\\ ~~~~~~~~= \boxed{(x+3)/(x-1)}`