Answer:
Given the statement:
8,000 earn in four years compounded daily at 5%
To find the amount we use formula:
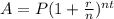
where P is the principal , A is the amount , n is number of times compounded per year and t is the time in year.
Here, Principal(P) = $8000, r = 5% and n = 365
Substitute these given values we get;
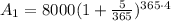

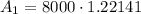
Simplify:
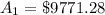
To find the Interest we use formula:
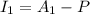
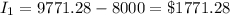
It is also given that:
8,000 earn in four years compounded annually at 5%.
Here, P = $8000, r = 5% , t =4 year and n = 1
Using the same formula to calculate the amount:


Simplify:
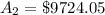
To find the Interest :
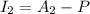
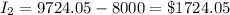
Then;

Therefore, $47.23 more would $8,000 earn in four years compounded daily at 5% than compounded annually at 5%