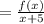Answer:
1. If x = -5 is a root of f(x), then (x + 5) must be a Factor of f(x).
2. Find the Quotient of f(x) when f(x) is divided by (x + 5).
3. Then Remainder of this operation is 0.
4. Thus, (x + 5) is Factor f(x).
5. Therefore, x = -5 is a root of f(x).
Remainder Theorem States that
→→Divisor = Dividend × Quotient + Remainder
→ f(x)= (x+5)×Quotient +0
→f(x)=Quotient× (x+5)
Quotient