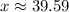Answer:
B. 39.59
Explanation:
So 43 degrees, you know the length of the opposite side (27) and the angle (43 degrees), the only unknown is the hypotenuse. So you're looking for a trigonometric ratio that uses the angle (all of them do, except technically the inverse don't), the opposite side, and the hypotenuse. Sine is defined as
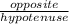 . So let's plug in known values:
. So let's plug in known values:
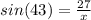
Multiply both sides by x
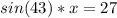
divide both sides by sin(43)
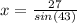
Normally I would use a calculator, but in this case I'll use the approximation given in the problem of 0.682
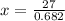
simplify the fraction