Answer:
(a)= option 3
(b)= option 3
Explanation:
(A) It is given that a sequence is defined by the recursive function
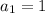 and
and
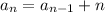
Now, substituting the value of n=2 in above equation,
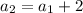
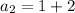
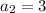
Again putting n=3,
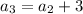
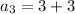
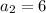
Putting n=4,
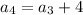

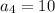
Putting n=5,
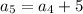
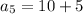
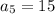
Putting n=6,
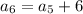
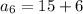
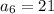
Putting n=7,
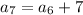
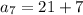
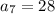
Hence, option 3 is correct.
(B) The given sequence is :
5, -10, 20, -40, 80.....
Since, the given sequence is GP, therefore
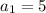 and r=-2
and r=-2
The nth term is given by:
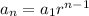
For fifteenth term, put n=15 in above equation, we get
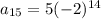
=
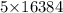
=
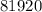
Hence, the fifteenth term is 81920.
Option 3 is correct.