Answer:
Options (1),(3),(4) are correct and Options (2) and (5) are incorrect.
Explanation:

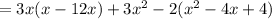
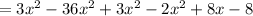
![=[tex]-32x^(2)+8x-8](https://img.qammunity.org/2020/formulas/mathematics/high-school/wzxsip0fj1840poprxwvgiz8sc7j63r7d4.png)
In this question we do the the simplification of term -2(x-2)^2 by squaring (x-2) then we find simplified product is not a binomial.
After multiplying, the like terms are combined by adding and subtracting.
The parentheses are eliminated through multiplication and then
The final simplified product is

Therefore Options (1),(3),(4) are correct and Options (2) and (5) are not correct.