Question

Which is the equation in slope-intercept form for the line that passes through (−2, 15) and is perpendicular to 2x + 3y = 4?

y=−32x+18

y=32x−12

y=23x+18

y=32x+18

Answer 1

y=3/2x + 18

Explanation:

So when two lines are perpendicular, that simple means the slope are reciprocals, and the signs are opposite. So for example if one equation had a slope of
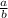`(a)/(b)`, the equation that is perpendicular, would have a slope of
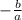`-(b)/(a)`. So the first step would be to find the slope of 2x+3y=4. To find the slope we can convert it into slope-intercept form which is y=mx+b where m is the slope, and this is done by isolating y, as you can see the y is alone in the slope-intercept form.

Original equation:

2x + 3y = 4

subtract 2x from both equations:

3y = -2x + 4

Divide both sides by 3

y = -2/3x + 4/3

The y-intercept doesn't really matter in this case, what really matters is the slope, and the slope is the coefficient of x, since as x increases by 1, it will increase by the amount of the coefficient, because the slope is rise/run and since the run is 1, if you increase x by 1, the run is the slope, which is the coefficient. The slope in this case is -2/3. So the reciprocal of the slope is 3/2 (notice how the sign is the opposite as well). Now we have the equation

y=3/2x + b

To find the y-intercept, you simply use the point that was given (-2, 15). Plug in -2 as x, and 15 as y to find the value of b

Original equation

y=3/2x + b

Plug in known values:

15 = 3/2(-2) + b

Multiply the fraction:

15 = -6/2 + b

Simplify the fraction:

15 = -3 + b

Add 3 to both sides

18 = b

This gives you the equation

y=3/2x + 18