Question

What is the approximate area of the shaded sector in the circle shown below

Answer 1

D. 25 inch²

Explanation:

We are given that,

Radius of the circle, r = 4.3 inches

Central angle made by the circle, θ = 155° = 2.705 radians

We have that,

Area of the sector =
`(r^2\theta)/(2)`

Substituting the values, we get,

Area of the sector =
`((4.3)^2* 2.705)/(2)`

i.e. Area of the sector =
`(18.49* 2.705)/(2)`

i.e. Area of the sector =
`(50.01545 )/(2)`

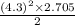
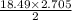
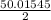
i.e. Area of the sector = 25.008 ≈ 25 inch²

Thus, the area of the shaded sector is 25 inch².

Hence, option D is correct.

Answer 2

Option (D)

Explanation:

The area of sector of a circle is given by formula:

Area of sector of circle= (
`r^(2)`∅)/2

where r is the radius of circle and ∅ is the angle subtended by the arc at the center of circle in radians.

Given :

∅ =155°

radius =4.3 in

The first step will be to convert the angle from degree to radian

According to formula:

`\pi radian = 180`°

Using above to solve:

`155`°=
`\pi/180`×155° = 2.705 radians

Area of sector of circle= (
`r^(2)`∅)/2

Substituting value into above we have,

Area of sector of circle= (
`4.3^(2)` ×2.705)/2 = 25.007 = 25
`in^2`(approx)

So the answer is Option (D)