Question

Find the coefficient of x^7y^3 in the expansion of (x - 2y)^10

Answer 1

-960

Explanation:

1) Expand
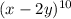`(x - 2y)^(10)` using the binomial theorem.

Binomial Theorem:
`\left(a+b\right)^n=\sum _(i=0)^n\binom{n}{i}a^(\left(n-i\right))b^i`

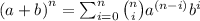
1.1) Substitute the values into the theorem.

`\sum _(i=0)^(10)\binom{10}{i}x^(\left(10-i\right))\left(-2y\right)^i`

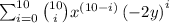
1.2) Expand summation.

`=(10!)/(0!\left(10-0\right)!)x^(10)\left(-2y\right)^0+(10!)/(1!\left(10-1\right)!)x^9\left(-2y\right)^1+(10!)/(2!\left(10-2\right)!)x^8\left(-2y\right)^2+(10!)/(3!\left(10-3\right)!)`

`x^7\left(-2y\right)^3+(10!)/(4!\left(10-4\right)!)x^6\left(-2y\right)^4+(10!)/(5!\left(10-5\right)!)x^5\left(-2y\right)^5+(10!)/(6!\left(10-6\right)!)x^4\left(-2y\right)^6+(10!)/(7!\left(10-7\right)!)x^3\left(-2y\right)^7+(10!)/(8!\left(10-8\right)!)x^2\left(-2y\right)^8+(10!)/(9!\left(10-9\right)!)x^1\left(-2y\right)^9+(10!)/(10!\left(10-10\right)!)x^0\left(-2y\right)^(10)`

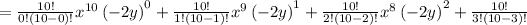
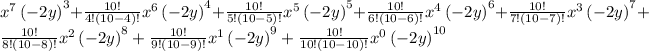
1.3) Simplify them.

1.4) You will get:

`=x^(10)-20x^9y+180x^8y^2-960x^7y^3+3360x^6y^4-8064x^5y^5+13440x^4y^6-15360x^3y^7+11520x^2y^8-5120xy^9+1024y^(10)`

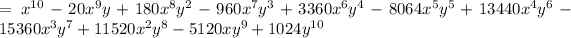
2) We are told to find the coefficient of
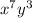`x^(7) y^(3)`. Find it from the simplified expansion. The coefficient is -960.