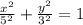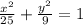Question

Find the equation of the ellipse with the following properties.

The ellipse with foci at (4, 0) and (-4, 0); y-intercepts (0, 3) and (0, -3).

Answer 1

The equation of ellipse is
`(x^2)/(25)+(y^2)/(9)=1`.

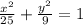Explanation:

The center of ellipse is origin because the ellipse has foci at (4, 0) and (-4, 0); y-intercepts (0, 3) and (0, -3).

The general equation of an ellipse is

`(x^2)/(a^2)+(y^2)/(b^2)=1`

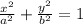
Where, a is major axis and b is minor.

The y-intercepts are (0, 3) and (0, -3). So, the value of b is 3.

The foci of ellipse is
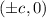`(\pm c,0)`.The relation between foci and major, minor axis is

`c^2=a^2-b^2`

`(4)^2=a^2-(3)^2`

`16=a^2-9`

`a^2=25`

`a=5`

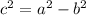
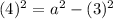
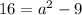
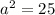
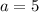
The equation of ellipse is

`(x^2)/(5^2)+(y^2)/(3^2)=1`

`(x^2)/(25)+(y^2)/(9)=1`