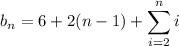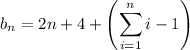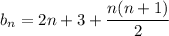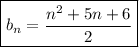Question

The math question is on the image
find the nth term of the sequence ​

Answer 1

28balls

Explanation:

according to me:

from pattern 1 to 2 four balls were added

from 2 to 3 five balls were added

from 3 to 4 6 balls were added

so you can see that there is a certain sequence that is coming up

that is 4,5,6 so just added 7.

so 21 plus other 7 balls will give us 28 balls

Answer 2

Notice how Pattern 2 is Pattern 1 with 4 balls added in the bottom row.

Pattern 3 is Pattern 2 with 5 more balls.

Pattern 4 is Pattern 3 with 6 more balls.

Generalizing the trend, we expect Pattern
`n` to be identical to Pattern
`n-1` with
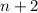`n+2` more balls.

If
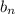`b_n` is the number of balls in the
`n`-th pattern, then we have the recursive relation

`\begin{cases} b_1 = 6 \\ b_n = b_(n-1) + n + 2 & \text{for } n>1 \end{cases}`

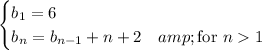
We can solve this recurrence by substitution. Using the definition of
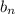`b_n`, we have

`b_(n-1) = b_(n-2) + (n-1) + 2 \\\\ \implies b_n = (b_(n-2) + (n-1) + 2) + n + 2 \\\\ \implies b_n = b_(n-2) + 2*2 + \bigg(n + (n-1)\bigg)`

`b_(n-2) = b_(n-3) + (n-2) + 2 \\\\ \implies b_n = (b_(n-3) + (n-2) + 2) + 2* 2 + \bigg(n + (n-1)\bigg) \\\\ \implies b_n = b_(n-3) + 3*2 + \bigg(n + (n-1) + (n-2)\bigg)`

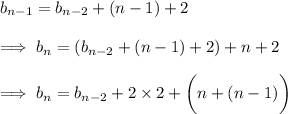
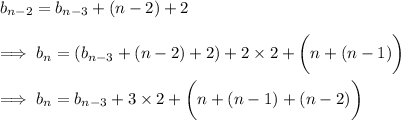
and so on, down to

`b_n = b_1 + (n-1)*2 + \bigg(n + (n-1) + (n-2) + \cdots + 2\bigg)`

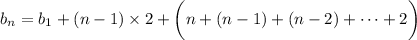
Recall that

`\displaystyle \sum_(i=1)^n i = 1 + 2 + 3 + \cdots + n = \frac{n(n+1)}2`

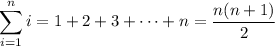
Then we find

`\displaystyle b_n = 6 + 2(n-1) + \sum_(i=2)^n i`

`\displaystyle b_n = 2n + 4 + \left(\sum_(i=1)^n i - 1\right)`

`\displaystyle b_n = 2n + 3 + \frac{n(n+1)}2`

`\displaystyle \boxed{b_n = \frac{n^2+5n+6}2}`