Answer:
(A) and (D)
Explanation:
It is given that the given expression
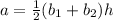 can be used to determine the area, a, of a trapezoid with height, h, and base lengths
can be used to determine the area, a, of a trapezoid with height, h, and base lengths
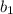 and
and
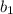 .
.
Thus, solving the given equation and finding the value of
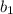 , we get
, we get
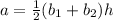
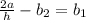
And the expression for height is:
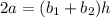

(A) The given expression is:
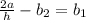
which is equivalent to the given expression, therefore this option is correct.
(B) The given expression is:
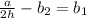
which is not equivalent to the given expression, therefore this option is not correct.
(C) The given expression is:
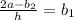
which is not equivalent to the given expression, therefore this option is not correct.
(D) The given expression is:

which is equivalent to the given expression, therefore this option is correct.
(E) The given expression is:
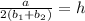
which is not equivalent to the given expression, therefore this option is not correct.