2 Answers

Ivan Zuzak · Answer 1 · 2020-01-22T12:57:10+0000

Answer:

(D) 2.11

Explanation:

The given expression is:

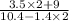
$\frac{3.5{*}2+9}{10.4-1.4{*}2}$

Simplifying the above given expression, we get

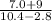
(7.0+9)/(10.4-2.8)

=
(16)/(7.6)

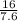
Multiplying and dividing the above expression with 10, we get

=
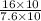
$\frac{16{*}10}{7.6{*}10}$

=
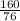
(160)/(76)

=
(40)/(19)

=
2.11

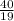
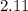
Hence, the simplified value of the given expression is 2.11, and thus option D is correct.

Please log in or register to add a comment.