For this case we must indicate which of the options given is a factor of the following polynomial:
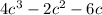
If we take common factor of the terms we have:

Within the parenthesis we have
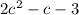 , then:
, then:
The term of the medium is rewritten as a sum of two terms, whose multiplication is
 and the sum is -1. These numbers are:
and the sum is -1. These numbers are:
-3 and 2
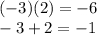
So;
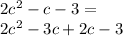
Factoring for each group we have:
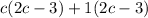
This is equivalent to:
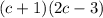
Thus,
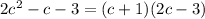
Then,
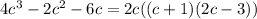
Thus, a factor of the polynomial is
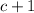
Answer:
Option A