Question

Identify which technique would be best applied to factor the polynomial below.

Answer 1

A

Explanation:

For factoring, if we can ever right a factor as
`(a)^2` and another as
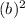`(b)^2` with a MINUS in between them, then the technique of "difference in two squares" is perfect!

From the problem shown, we can actually do this (shown below):

`x^2-25\\=(x)^2-(5)^2`

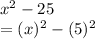
The rule is
`a^2-b^2=(a+b)(a-b)`

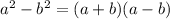
Thus the problem reduces to:

`(x)^2-(5)^2\\=(x+5)(x-5)`

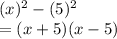
We have use "difference of two squares" here, hence answer choice A is right.