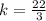Question

If the graph of


`f(x) = \frac{9x { }^(2) + 37x + 4 }{3x + 5}`
has an oblique asymptote at y=3x+k, what is the value of k?

Answer 1

Answer with explanation:

`f(x)=(9x^2+37x+4)/(3x+5)`

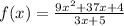
Since the degree in the numerator is greater than degree of Denominator .To find the Oblique asymptote we will divide numerator by denominator.

Quotient

`=3x+(22)/(3)`

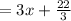
--------------------------------(1)

Also, Given Oblique Asymptote

y=3x+k-----------(2)

Now,Equating (1) and (2)

`k=(22)/(3)`

Answer 2

Answer: k = 22/3

You can use polynomial long division to get the answer.

See attached image below.