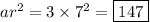The first few terms of a geometric sequence with first term
 and common ratio
and common ratio
 look like
look like
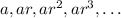
and so on. Notice that the
 -th term (where
-th term (where
 is a natural number) is
is a natural number) is
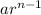 .
.
For this particular sequence, the first term is
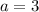
and the fourth term is
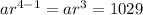
Substitute
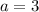 into the second equation and solve for
into the second equation and solve for
 .
.
![3r^3 = 1029 \implies r^3 = 343 \implies r = \sqrt[3]{343} = \sqrt[3]{7^3} = 7](https://img.qammunity.org/2023/formulas/mathematics/high-school/t40nfpih8u9mi47y8tsqrc2n8zwnw846bs.png)
Then the two terms between the 1st and 4th - i.e. the 2nd and 3rd terms - are
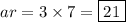
and