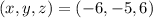I assume the third equation is supposed to be
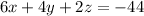 . We can divide both sides by 2 right away to simplify it a bit,
. We can divide both sides by 2 right away to simplify it a bit,
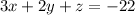 .
.
To start, the system in augmented-matrix form is
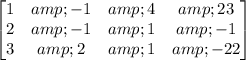
Subtract 2 times row 1 from row 2, and 3 times row 1 from row 3:
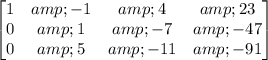
Subtract 5 times row 2 from row 3:
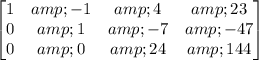
Multiply row 3 by 1/24:
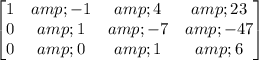
Add 7 times row 3 to row 2:
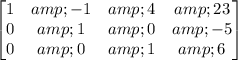
Add row 2 and -4 times row 3 to row 1:
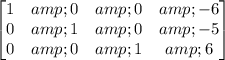
Then the solution to the system is