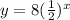Answer:
Yes
Explanation:
Katie's Graph equation:
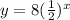
Another graph equation:
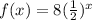
Since the right hand side of both the equations of graphs are equal
So, Left hand side of both equations of graphs must be equal
So, :
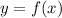
So, the graph of
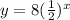 is the same as the graph of
is the same as the graph of
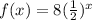
Refer the attached figure
Purple line :
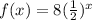
Red line :