Question

What is the quadratic function that is created with roots -3 and 1 and a vertex at (-1, -8)

Answer 1

`y=2(x+1)^2-8`

Explanation:

To write the quadratic equation, begin by writing it in vertex form

`y = a(x-h)^2+k`

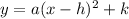
Where (h,k) is the vertex of the parabola.

Here the vertex is (-1,-8). Substitute and write:

`y=a(x--1)^2+-8\\y=a(x+1)^2-8`

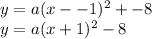
To find a, substitute one point (x,y) from the parabola into the equation and solve for a. Plug in (1,0) a x-intercept of the parabola.

`0=a((1)+1)^2-8\\0=a(2)^2-8\\0=4a-8\\8=4a\\2=a`

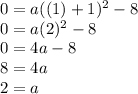
The vertex form of the equation is
`y=2(x+1)^2-8`.