I think factorizing everything you can first will make the simplification ... well, simpler.

The factors of
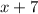 in the second rational expression cancel:
in the second rational expression cancel:
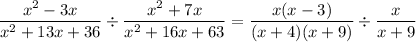
Now, use the property
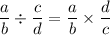
(this is the property of multiplication having to do with multiplicative inverse, or "inverting the divisor" as the question calls it) to write
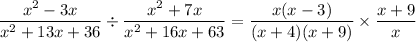
and we see some more cancellation, namely of the factors of
 and
and
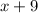 .
.
