Question

Find an equation in standard form of the parabola that passes through (-2, 9), (-4, 5), and (1, 0)

Answer 1

y=-1x^2 -4x +5

Explanation:

Given points (-2, 9), (-4, 5), and (1, 0)

General quadratic equation is y=ax^2 +bx+c

plug in each point and frame three equations

(-2,9)

`9=a (-2)^2+b(-2) + c`

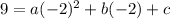
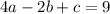`4a-2b+c=9` equation 1

(-4,5)

5 = 16a -4b+c equation 2

(1,0)

0= a + b + c equation 3

Use equation 1 and 3

multiply third equation by -1 and then add it with equation 1

4a - 2a + c = 9

-a -b -c = 0

---------------------

3a - 3b = 9

divide whole equation by 3

a - b = 3 equation 4

use equation 2 and 3

16a -4b+c = 5

-a -b -c =0

------------------------

15a -5b = 5

divide whole equation by 5

3a -b= 1 equation 5

use equation 4 and 5 . multiply equation 5 by -1

-3a +b =-1

a - b = 3

-----------------------

-2a = 2

a= -1

plug it in equation 4 and find out b

a - b = 3

-1 - b = 3

add 1 on both sides

-b = 4 so b= -4

Now plug in the values and find out c

a + b+c = 0

-1 -4 + c= 0

-5 +c =0

c=5

Now plug in the values in the general equation

y=ax^2 +bx+c

y=-1x^2 -4x +5