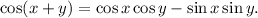Question

Which sum or difference identity could be used to prove that cos(pi+q)=-sin q is an identity?

Answer 1

Answer: The answer is
`\cos(x+y)=\cos x\cos y-\sin x\sin y.`

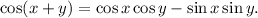
Step-by-step explanation: We are to find the sum or the difference that could be used to prove the following identity:

`\cos(\pi+q)=-\cos q.`

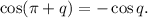
To prove the above identity, the following sum which results in a difference, will be appropriate

`\cos(x+y)=\cos x\cos y-\sin x\sin y.`

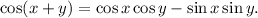
The proof is as follows

`L.H.S.\\\\=\cos(\pi+q)\\\\=\cos \pi\cos q-\sin \pi\sin q\\\\=(-1)\cos q-0* \sin q\\\\=-\cos q\\\\=R.H.S.`

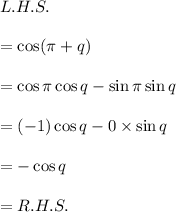
Thus, the answer is
`\cos(x+y)=\cos x\cos y-\sin x\sin y.`