Answer:
B) All the real numbers except 4.
Explanation:
The given rational expression f(x) =
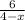
To find the domain of the rational function, first we have to find the restricted domain.
To find the restricted domain set the denominator equal to zero.
4 - x = 0
x = 4
The restricted domain is at x = 4.
Which means the function does not exist when x = 4. When we plug in x =4 in the rational function, we get the denominator is 0.
Therefore, the function does not exist at x =- 4.
This means except 4 all the real numbers are the domain.
Hope this will help you to understand the concept.
Answer: B) All the real numbers except 4.
Thank you.